自在錐で円形の穴をあけたいときや、モーターで円筒状のものを回したいときなど、DIYや工作の中で円の中心や直径がわかると便利だな~と思うシーンがしばしばあるとおもいますが・・・

単純に定規を当てるだけでは、正確な直径や円の中心を求めることは不可能なんですよね~。
でも、数学のある定理を利用すると、身近にあるもので円の中心や直径を限りなく正確に求めることが可能なので、その方法をご紹介します(^^)/
指矩(さしがね)と円周角の定理を使って円の直径を求める
とりあえず、今回はコピー用紙に円を描いてみました。
この円の中心や直径を求めていきたいと思いますが・・・

①まず、直角のある物を円の外周の任意の3点と接するように置きます。
今回は円を描いたコピー用紙を折り曲げて、円の外周にぴったり合うようにしてみました。

※できれば指矩(さしがね)などの直角の信頼性の高いものを使うことをオススメします。
②紙の辺と円の外周でできた二つの接点を直線で結びます。

③作業はここまで。
実は先ほど引いた線が円の直径になっているので・・・

線の長さを測れば円の直径を求めることができ・・・
また直径の半分の位置に印をつければ、そこが円の中心となります(●´∀`)人(´∀`●)
円周角の定理について
これは数学の「円周角の定理」ってやつを利用していまして・・・
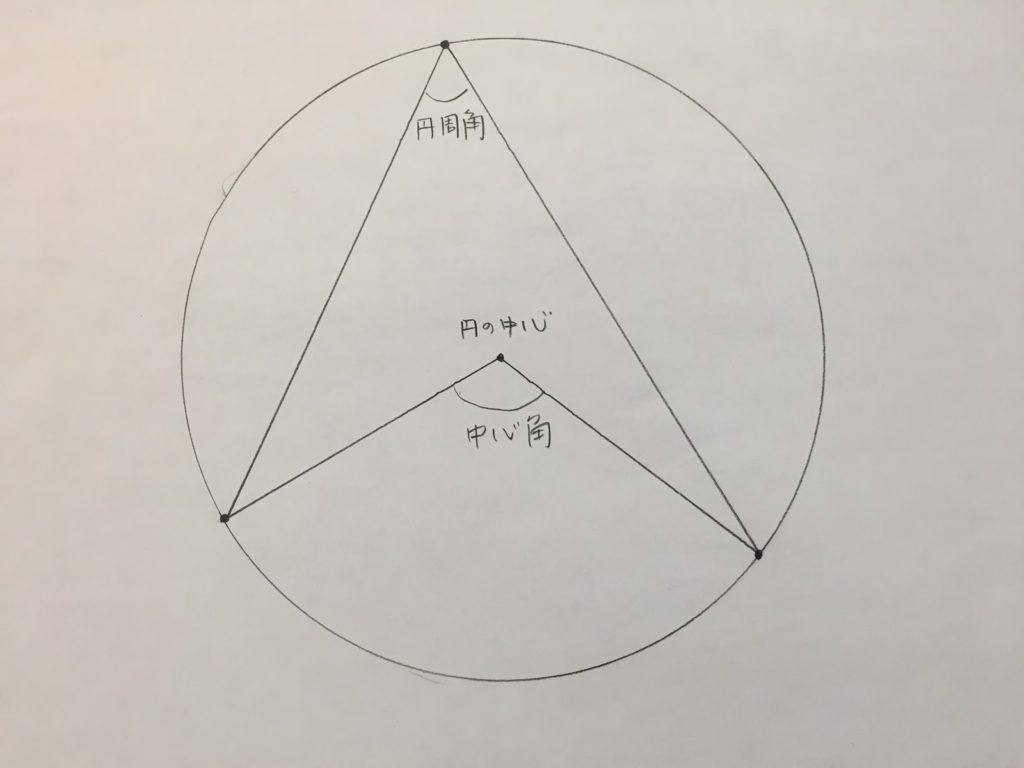
円周上の任意の3点を結んでできる角を「円周角」
円周上の任意の2点と円の中心を結んでできる角を「中心角」
と呼びます。
円周上の同じ2点から作られる円周角と中心角の関係は
「中心角は円周角の2倍になる」
という性質があります。
つまり円周角が30°なら、中心角は60°って具合です。
なので・・・
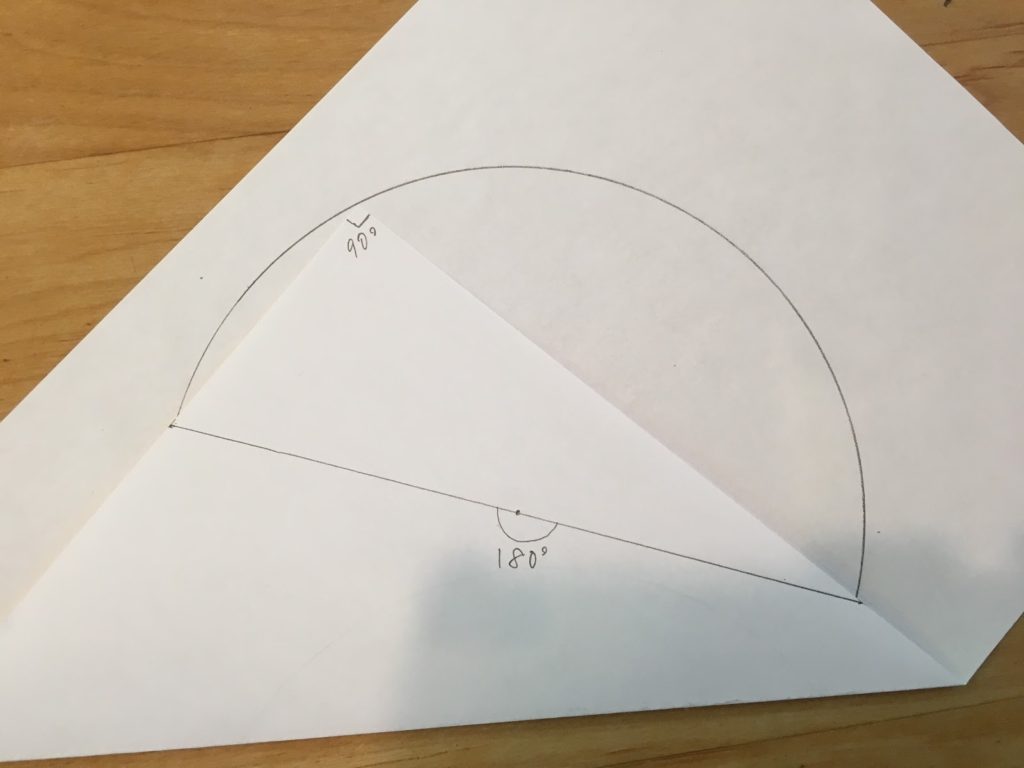
円周角が90°になるような円周上の2点が判れば、その2点と円の中心を結んでできる中心角は180°・・・
つまり「円の中心を通る直線=直径」となるわけです!
ちなみに、円周角の特徴として、円周角を作る時の2点が固定されていれば、円周角の頂点となる点はどの位置でも必ず同じ角度になる性質がありますので、直角の当て方はどんな形でもオッケーです(^^)/
円の中心がわからないときの中心の求め方で限りなく正確にもとめるのに便利な方法かな~と思いますので、ぜひ頭の片隅にでも留めておいてください♪( ´θ`)ノ
コンパスを用いてより正確な中心を求める方法
先ほどは円の中心を簡易的に定規で求めましたが、より正確な中心を見つけたい場合はコンパスを使って作図から求めていきます。
円の中心は直径の垂直二等分線を作図することで求めることが可能です。
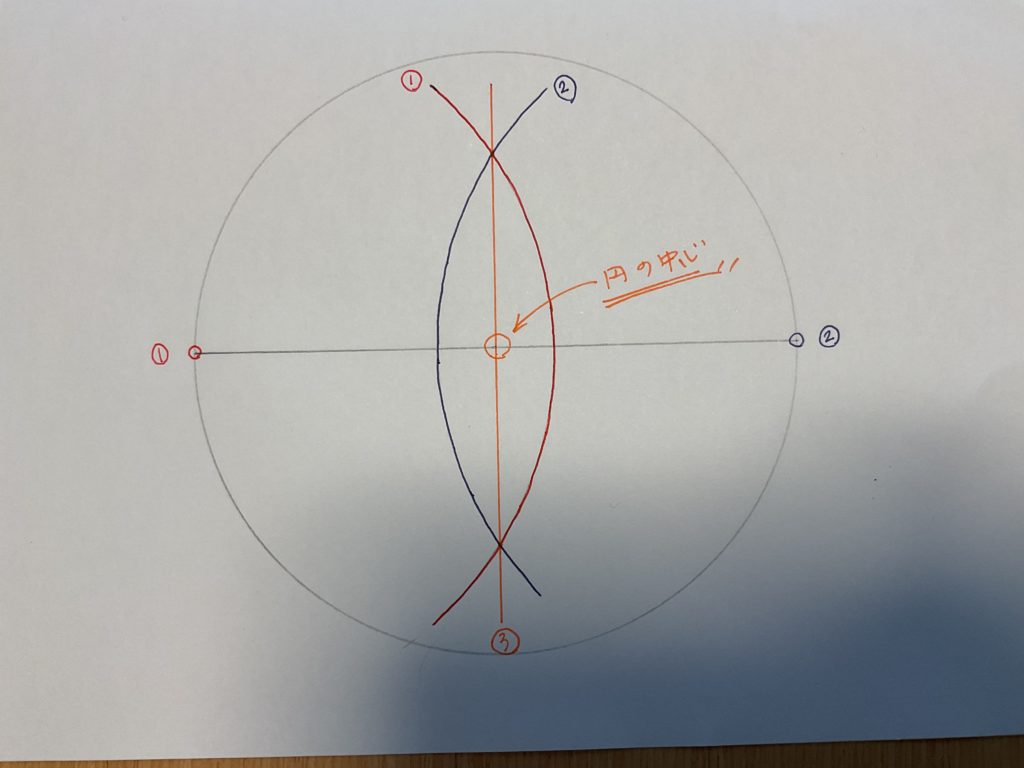
- 直径の左端①から半分よりコンパスで円を描く:赤(描く円の半径は元の円の半径より長くすること)
- 直径の右端②から①と同じ半径の円をコンパスで描く:青
- ①と②で描いた円の交点(2箇所)を通る直線を描く(円の直径の垂直二等分線)
- 円の直径と③で描いた直線の交点が円の中心となる
この作図方法が線分の垂直二等分線の作図方法です。今回は「垂直」というところは無関係ですが、「直径を二等分する線(点)」を作図により求めることができれば、そこが円の中心となるわけです。
「円周角の定理」「線分の垂直二等分線の作図」どちらも中学校で習う知識で、こんなの習っても使う機会あんの?なんて当時は思ってましたが、、、意外と使う機会ってあるもんなんですね(๑´∀`๑)」
オツカレサマ( ^^) _旦~~



























コメント